Debugging

Step-by-step debugging

Learning Objectives

Understand how to run a script under debugger control
Understand how to use the debugger to stop execution at certain points
Understand how to use the debugger to step through a program

The following assumes that we have the files histograms.py and do_equalization.py in our current directory, together with the example image Unequalized_Hawkes_Bay_NZ.png. The file histograms.py defines two functions a function plot_histogram and a function equalize. The function plot_histogram plots the histogram of data values in an array and the cumulative distribution of this histogram on top of it. The equalize function is meant to perform the algorithm of histogram equalization on a grayscale image:

def equalize(image, n_bins=256):
    """
    Perform histogram equalization on the given grayscale ``image`` (2D array
    of intensity values between 0 and 1), using ``n_bins`` bins for the
    histogram.
    Returns the equalized image.
    """
    bins = numpy.linspace(0, 1, n_bins, endpoint=True)
    bins, hist = numpy.histogram(image.flatten(), bins=bins, density=True)
    cdf = hist.cumsum() / n_bins
    # Invert the CDF by using numpy's interp function
    equalized = numpy.interp(image.flatten(), bins, cdf)

    # All this was performed on flattened versions of the image, reshape the
    # equalized image back to the original shape
    return equalized.reshape(image.shape)

The main idea behind the algorithm is that we want to transform the image using a mapping that preserves the relative values of the intensities but use all the values in the intensity range for an (approximately) equal amount of pixels. It turns out that inverting the cumulative distribution function of the intensity values gives us such a mapping.

With that in mind, the algorithm has the following steps:

Calculate the histogram of the grayscale values (between 0 and 1)
Calculate the cumulative distribution of these values
Interpret the cumulative distribution as a function and invert it, then use that inverted function to get the new intensity values.

As a result, the equalized image should have a flat histogram of intensity values and equivalently a linear cumulative distribution of intensity values from 0 to 1.

Let’s try to run the do_equalization.py script which plots an example image and its histogram, equalizes it using the above function and plots the result:

% run do_equalization.py

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
[..]/do_equalization.py in <module>()
     16
     17     # Equalize the image histogram
---> 18     equalized = histograms.equalize(image)
     19     plt.subplot(2, 2, 3)
     20     plt.imshow(equalized, cmap='gray')

[..]/histograms.py in equalize(image, n_bins)
     16     cdf = hist.cumsum() / n_bins
     17     # Invert the CDF by using numpy's interp function
---> 18     equalized = numpy.interp(image.flatten(), bins, cdf)
     19
     20     # All this was performed on flattened versions of the image, reshape the

[..]/function_base.py in interp(x, xp, fp, left, right, period)
   1269             return compiled_interp([x], xp, fp, left, right).item()
   1270         else:
-> 1271             return compiled_interp(x, xp, fp, left, right)
   1272     else:
   1273         if period == 0:

ValueError: fp and xp are not of the same length.

OK, apparently that did not work. The arguments to numpy.interp do not seem to have the same length. Let’s use the debugger to investigate this:

% debug


ipdb> xp.shape
(99,)
ipdb> fp.shape
(100,)
ipdb> u
> [...]/histograms.py(18)equalize()
     16     cdf = hist.cumsum() / n_bins
     17     # Invert the CDF by using numpy's interp function
---> 18     equalized = numpy.interp(image.flatten(), bins, cdf)
     19
     20     # All this was performed on flattened versions of the image, reshape the

ipdb> bins.shape
(99,)
ipdb> cdf.shape
(100,)
ipdb> q

So it seems that bins and cdf that we provide to numpy.interp differ in their length by one. This is a typical thing to happen when dealing with histograms, since we sometimes use bins (N values) and sometimes bin edges (N+1 values). Let’s fix this, by removing the last value of the cdf variable:

def equalize(image, n_bins=256):
    bins = numpy.linspace(0, 1, n_bins, endpoint=True)
    bins, hist = numpy.histogram(image.flatten(), bins=bins, density=True)
    cdf = hist.cumsum() / n_bins
    # Invert the CDF by using numpy's interp function
    equalized = numpy.interp(image.flatten(), bins, cdf[:-1])

    # All this was performed on flattened versions of the image, reshape the
    # equalized image back to the original shape
    return equalized.reshape(image.shape)

Jupyter notebooks and external files

The jupyter notebook is best suited to a programming style where all the code that is changed is included in the notebook: after a change to a function, the re-execution of the respective cell will update its definition. For more complex projects with functions defined in external files, there is a problem, though: Python only imports a module once, therefore if we edit the external file (e.g. in a text editor), then those changes are not taken into account, we will still use the version of the module when we (or another script/function) first imported it. This behavior can be very confusing… There are various ways to deal with this problem, but probably the easiest is to force the reload of all modules for every code execution:

%load_ext autoreload
%autoreload 2

Reloading modules remains a tricky issue, though. If it fails, the easiest might be to restart the kernel of the current notebook and to re-execute all cells.

Let’s run the script again:

% run do_equalization.py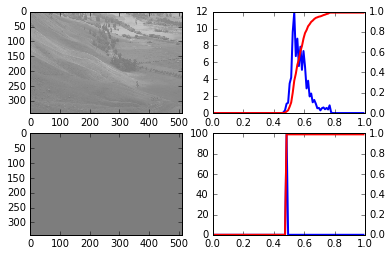

do_equalization output 1

Um, well, the script now runs without an error message but the result does not look any good. We don’t have an error that we can debug in a post-mortem way so instead we start the complete script under debugger control:

% run -d do_equalization.py

Breakpoint 1 at [...]/examples/do_equalization.py:1
NOTE: Enter 'c' at the ipdb>  prompt to continue execution.
> [...]/do_equalization.py(1)<module>()
1---> 1 import matplotlib.pyplot as plt
      2
      3 import histograms
      4
      5 if __name__ == '__main__':

ipdb>

As when using %debug, we now have a debugger prompt but now we are at the start of the script. The most important commands are the following:

n (next): Execute the current line and step over it (i.e. stay on the same level)
s (step): Execute the current line by stepping into functions called on the line
c (continue): continue execution until the end of a script, an uncaught exception or a breakpoint (see below)
b (breakpoint): create a new breakpoint at a given line number (and optionally in a given file)

Just pressing return at the prompt will execute the previous command again (useful for n, s, c).

Debugging without IPython/Jupyter notebook

In some situations you cannot use IPython, for instance to debug a script that wants to be called from the command line. In this case, you can call the script with python -m pdb script.py or python -m ipdb scrip.py (needs an installation of ipdb):

$ python -m pdb do_equalization.py

> [...]/do_equalization.py(1)<module>()
-> import matplotlib.pyplot as plt
(Pdb)

We are interested in the code happening in the equalize function, so we’ll set a breakpoint at its first line and continue our execution until then:

ipdb> b histograms.py:20
Breakpoint 2 at [...]/histograms.py:20
ipdb> c
> [...]/histograms.py(20)equalize()
     18     Returns the equalized image.
     19     """
2--> 20     bins = numpy.linspace(0, 1, n_bins, endpoint=True)
     21     bins, hist = numpy.histogram(image.flatten(), bins=bins, density=True)
     22     cdf = hist.cumsum() / n_bins

ipdb> n
> [...]/histograms.py(21)equalize()
     19     """
2    20     bins = numpy.linspace(0, 1, n_bins, endpoint=True)
---> 21     bins, hist = numpy.histogram(image.flatten(), bins=bins, density=True)
     22     cdf = hist.cumsum() / n_bins
     23     # Invert the CDF by using numpy's interp function

ipdb> bins[:10]
array([ 0.        ,  0.01010101,  0.02020202,  0.03030303,  0.04040404,
        0.05050505,  0.06060606,  0.07070707,  0.08080808,  0.09090909])
ipdb> n
> [...]/histograms.py(22)equalize()
2    20     bins = numpy.linspace(0, 1, n_bins)
     21     bins, hist = numpy.histogram(image.flatten(), bins=bins, density=True)
---> 22     cdf = hist.cumsum() / n_bins
     23     # Invert the CDF by using numpy's interp function
     24     equalized = numpy.interp(image.flatten(), bins, cdf[:-1])

ipdb> hist[:10]
array([ 0.        ,  0.01010101,  0.02020202,  0.03030303,  0.04040404,
        0.05050505,  0.06060606,  0.07070707,  0.08080808,  0.09090909])
ipdb> bins[:10]
array([ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.])

We have found the issue: we swapped the arguments for the return value of numpy.histogram, storing the bin edges in the hist variable and the histogram in bin. Looking back at our previous fix for the inconsistent length of bin and cdf we could have realized back then that bins should have 1 element more than cdf and not the other way round… Fixing those issues leads to the following code:

def equalize(image, n_bins=256):
    bins = numpy.linspace(0, 1, n_bins, endpoint=True)
    hist, bins = numpy.histogram(image.flatten(), bins=bins, density=True)
    cdf = hist.cumsum() / n_bins
    # Invert the CDF by using numpy's interp function
    equalized = numpy.interp(image.flatten(), bins[:-1], cdf)

    # All this was performed on flattened versions of the image, reshape the
    # equalized image back to the original shape
    return equalized.reshape(image.shape)

Now our script runs and gives the expected result:

% run do_equalization.py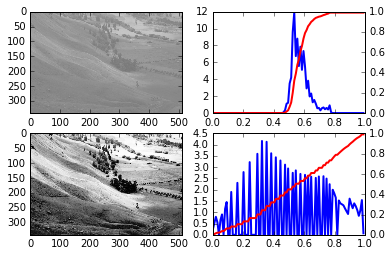

do_equalization output 2

Debug step by step

Call the check_data function from the previous section with numpy.nan as its target argument. The result is not as expected, use the debugger to go through the code step by step and find the problem.